How to precisely calculate large block-out volumes with a triple integral or handy chart
A common calculation in precast concrete manufacturing is determining the volume of a round blockout in a manhole wall. A round blockout is a hole either cast or cored into the side of a manhole wall. Mathematically, there are several methods to calculate this volume, ranging from a simple geometric formula to the theory-intensive calculus method.
The complex shape made by the blockout requires the use of upper-level mathematics and/or 3D CAD, which are two of only a few means for precisely calculating the volume of the blockout. Even armed with the calculus formula or 3D CAD, a specialized computer program or calculator that can solve integrals will be needed to calculate the final value. The key word in this approach is calculating “precisely.”
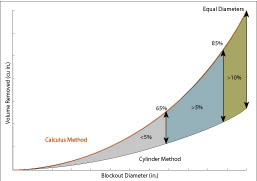
Figure 1.
A 5% error between the cylinder method and calculus method manifests itself once the diameter of the blockout reaches 65% of the inside diameter of the manhole. The error then continues to grow to more than 9% when the diameter of the blockout reaches 85% of the inside diameter of the manhole (see Figure 1). This difference in volume between the two methods is small when looking at the difference in weights. The cylinder method is still close enough to continue to use for blockout weight approximations (see Figure 2).
When to use the cylinder or calculus method
The formula for a cylinder (πr2h), where r is the radius of the blockout hole and h is the wall thickness, can be used to approximate the volume of a blockout. This will be referred to as the “cylinder method” and is close enough if you need a quick and easy calculation.
The “calculus method” uses a triple integral to determine a precise volume. The calculus method must use specific software or certain scientific calculators for a numerical answer. Using these tools, an equation can be derived specific to each manhole for different sizes of blockouts. Using these formulas, it is possible to get more precise answers than with the cylinder method.
When coring or using a blockout to form a 12-in.-diameter hole in a 48 -in. inside diameter (I.D.) manhole, it makes little difference whether the cylinder method or the calculus method is used to solve for the volume. However, change the blockout size to a 36-in.-diameter hole in the same 48-in.-I.D. manhole, and the difference in volume between the two methods starts to differ significantly as shown in the following examples.
Example 1. Calculate the volume for a 12-in.-diameter hole to be cast or cored in a 48-in.-I.D. manhole with a 5-in. wall thickness.
Cylinder formula
Volume = πr2h = (3.1416)(6 in.)2(5in.) = 565.49 in.3
Calculus method
Calculus solution
Volume = 569.2 in.3
Example 2. Calculate the volume for a 36-in.-diameter hole to be cast or cored in a 48-in.-I.D. manhole.
Cylinder formula
Volume = πr2h = (3.1416)(18 in.)2(5 in.) = 5,089.4 in.3
Calculus solution
Volume = 5,456.64 in.3
Then there are the tapered blockout holes – and a calculus formula for that as well. However, there is also a simpler method. If a blockout tapers from 26 in. to 24 in. in diameter, solve for the average of the two (25-in. diameter) in this case. Using the average diameter will produce an accurate approximated volume.
Conclusion
Comparing the results of the two examples, one can note the volume difference between the cylinder method and calculus method. The cylinder method is and will continue to be the fast and easy method to getting a quick volume that is close enough. Having said that, the actual difference in weight between the two formulas could be as much as 1,000 lbs when considering an 8-ft round manhole with two large-diameter blockouts. Admittedly, there is not a significant weight difference between the two formulas throughout the normal range of blockout sizes on most manhole sizes produced. For those who desire to calculate precisely how much concrete is removed due to a blockout, the difference may seem more significant.
The derived equations for each round product line are listed below. These equations deliver answers that are very close in volume but not exact. The equations should yield answers that are accurate to within 1% of the actual volume. In addition, if you just want to use a quick reference and not worry about a calculation, one with precise volume calculations using the calculus method is shown in the accompanying chart.
Eric Barger is vice president of C.R. Barger & Sons Inc., Lenoir City, Tenn.
References
Howard, Rebecca. Wall Volume from Hollow Cylinder – No Taper. 2010, from
www.PrecastWorld.com.
Derived volume equations:
48”Ø y = 0.0394×3 + 2.2728×2 + 20.337x – 46.043
60”Ø y = 0.0381×3 + 2.71×2 + 31.02x – 91.24
72”Ø y = 0.0331×3 + 3.516×2 + 35.409x – 122.6
84”Ø y = 0.0331×3 + 3.9561×2 + 49.01x – 202.86
96”Ø y = 0.036×3 + 4.0295×2 + 76.234x – 379.22
120”Ø y = 0.0329×3 + 5.2785×2 + 102.99x – 635.59
144”Ø y = 0.0294×3 + 5.8833×2 + 128.6x – 949.62
Assumed wall thickness:
48”Ø – 5”
60”Ø – 6”
72”Ø – 7”
84”Ø – 8”
96”Ø – 9”
120”Ø – 11”
144”Ø – 12”
Hole volume for Round Structures
Figure 2.

Leave a Reply